Abstract
We present improvements to several core numerical scheme in the Caelus library that are a first step in improving robustness and accuracy for meshes with less than optimal quality. Three general algorithms were improved:
- Interpolation schemes
- Non-orthogonal correction on the boundaries
- Gradient reconstruction
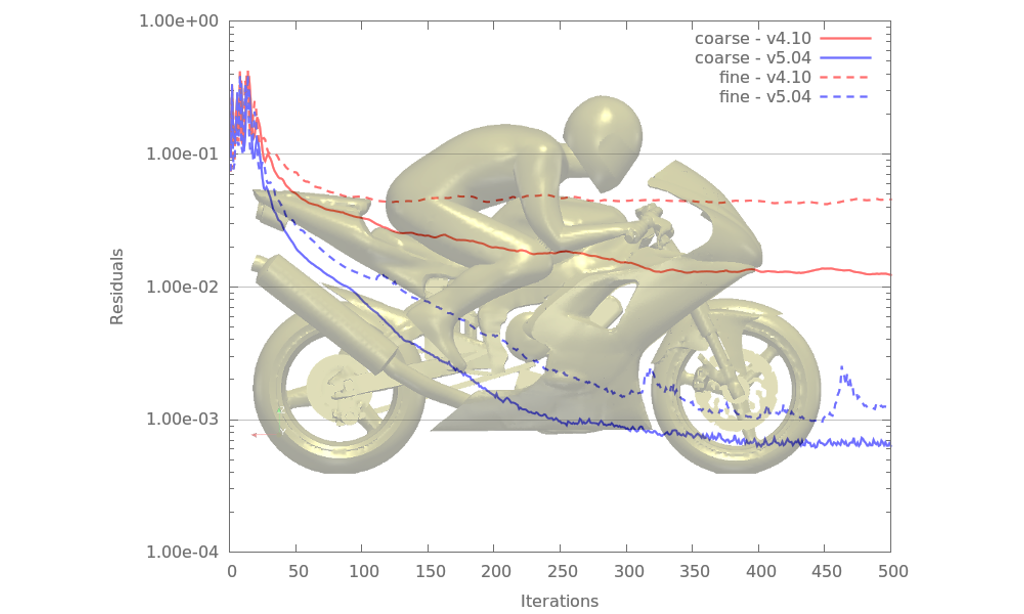
The interpolation schemes available in Caelus v4.10 are one-dimensional in nature. One-dimensional interpolation has difficulty on skewed cells where the cell center vector deviates from the shared face center. To address the numerical difficulties arising from the interpolation deficiency, two classes of total variation diminishing (TVD), multi-dimensional schemes, based
on central and upwind weighting, were introduced. Within each class, several limiters are available. Furthermore, these interpolation schemes can be used in either a fully implicit manner or with a deferred correction. This suite of new interpolation schemes significantly improves the robustness of Caelus without compromising accuracy. Several examples will presented
demonstrating the improved robustness of the new interpolation schemes.
While non-orthogonal correction has always been available in Caelus, when enabled it was only applied to the internal mesh. The cells adjacent to boundaries had no non-orthogonal correction applied. Non-orthogonal correction on the boundaries has been corrected in Caelus v5.04 enabling second order accuracy at the boundaries. For fixed value boundary conditions, second order accuracy can be achieved with either Gauss or least squares (LSQ) gradient reconstructions. For fixed gradient boundary conditions, second accuracy was initially achieved only with the LSQ gradient reconstruction. The default Gauss gradient reconstruction is inaccurate due to the boundary face value estimation. To enable second order accuracy with a Gauss-type gradient reconstruction a new scheme called corrected Gauss was added to Caelus. The corrected Gauss scheme does so by iterating to achieve a better estimate of the boundary face value.